Um misterioso matemático chamado Srinivasa Ramanujan, nascido em 1887, em Erode, na Índia, criou teoremas surpreendentes. Em 1900, com treze anos, ele começou a estudar séries aritméticas e geométricas e a partir daí, Ramanujan criou maneiras próprias para trabalhar a matemática.
Em 1904, com 17 anos, Ramanujan estudou a série harmônica, S (1/n), e calculou a constante de Euler, até 15 casas decimais. Começou depois a estudar os números de Bernoulli onde fez descobertas importantes.
Os estudos do matemático nunca foram efetivamente publicados. O que existe da sua obra são essencialmente fórmulas e expressões matemáticas isoladas e rascunhos manuscritos.
Ramanujan dedicou-se a várias áreas de investigação, incluindo funções teta, mecânica estatística, álgebras, teoria probabilística de números, formas modelares, funções elípticas, multiplicações complexas, séries hipergeométricas, expansões, entre outras.
Teoria dos números
Suponhamos que p é um número primo e n é um inteiro positivo. Assim, por um teorema bastante conhecido da Teoria Elementar dos Números, a maior potência de p que divide n é igual a:
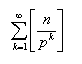
Nas descobertas elementares do Ramanujan consta que as frações contínuas dão uma excelente aproximação racional de II.
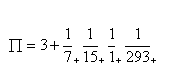
As sucessivas aproximações que equivalem à expansão decimal do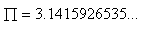 
através de 6 casas decimais. O aparecimento de um “grande” quarto quociente parcial, 293, é o primeiro responsável por este sucesso.
Ramanujan também oferece a aproximação:
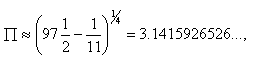
São muitas as contribuições do matemático, sendo ele considerado um gênio marcante para os estudos das ciências exatas. Ramanujan ensinou na Universidade de Madras e destacou-se na Trinity College, da Cambridge University, na Inglaterra, onde morou por alguns anos.
Conheça o filme sobre a vida de Srinivasa Ramanujan:
O Homem que viu o infinito
Tragicamente, o matemático contraiu tuberculose em 1917, e morreu em 1920, em Kumbakonam, na Índia.
